Example
Problem
In order to demonstrate how to use
the solver, consider the example problem
from Mathematica.com.
This is second order ODE or system of
two first order equations. 
In order to solve this equation, we
need to specify
- right hand side function (rhs)
- initial condition
- solvers parameters (optional)
RHS Function:
Inputs: First parameter double x; is
value of independent variable (time
in this example), second parameter double
*y is array of dependent variables,
size of array is specified by fourth
parameter int nSize.
Outputs: function calculate derivatives
double *ydot; of each dependent variable.
void rhs(double x, double *y, double *ydot, int nSize)
{
static double f = 700000;
static double R = 60;
static double L = 1e-4;
static double C1 = 1e-7;
static double C2 = 4e-10;
static double E0 = 0.1;
static double E = 0.2; //0.2 0.3
static double pi = 3.1415926535897932384626433832795;
ydot[0] = y[1];
ydot[1] = ( -R*y[1]-( (C2-C1)*fabs(y[0])/(2*C1*C2)
+(C1+C2)*y[0]/(2*C1*C2)+E0)+E*sin(2*pi*f*x))/L;
}
Solver initialization:
const int nSize = 2; //size of ODE system
CRungeKutta solver(nSize); //Create solver
double y[nSize] = {0, 0}; //Specify initial conditions
double t0 = 0; //specify initial value of independent variable
double t1 = 1.4e-4;//specify final value of independent variable
double t, dt, h;
double nSteps = 10000; //number of output points
solver.SetEps(1e-8);
t = t0;
dt = (t1-t0)/nSteps;
h = dt/100;
try
{
for(int i = 0; i<nSteps; i++)
{
solver.Solve(rhs, y, t0+i*dt, t0+(i+1)*dt,h);
printf("%e\t %e\t %e\n",t0+(i+1)*dt,y[0], y[1]);
}
}
catch(CError error)
{
printf("%s\n", error.ShowReason());
}
catch(...)
{
printf("Unknow Error\n");
};
return 0;
Solution:
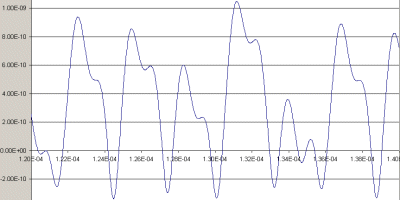
Download
source files - 4 Kb
Download project files - 6 Kb
|